徐勇研究組發現結構無序誘導的三維二階拓撲絕緣體

2021年05月24日 瀏覽次數: 0

      近日清華大學交叉信息研究院徐勇研究組在拓撲凝聚態物理領域取得重要進展，首次在理論上預言三維二階拓撲絕緣體可以在完全隨機點陣即無定形體系中存在，并發現結構無序可以誘發拓撲平庸相到二階拓撲絕緣體的量子相變。研究人員還提出在實空間中計算三維二階拓撲絕緣體拓撲不變量的方法（包括有時間反演對稱性的體系）。該成果的研究論文《結構無序誘導的三維二階拓撲絕緣體》（Structural-Disorder-Induced Second-Order Topological Insulators in Three Dimensions）于近日刊發于國際物理學期刊《物理評論快報》（Physical Review Letters）。

     最近，高階拓撲絕緣體在物理學的各個領域獲得廣泛關注。考慮一個維系統，這類新型拓撲絕緣體具有n-m( 1<m ≤ n)維無能隙邊界態。由于無定形材料在自然界中廣泛存在，一個很自然的問題是無定形系統中是否可以存在高階拓撲絕緣體。之前的研究表明三維二階拓撲絕緣體需要晶格對稱性保護。考慮到無定形系統沒有晶格對稱性，這似乎意味著三維系統中不能存在二階拓撲絕緣體。

                                      

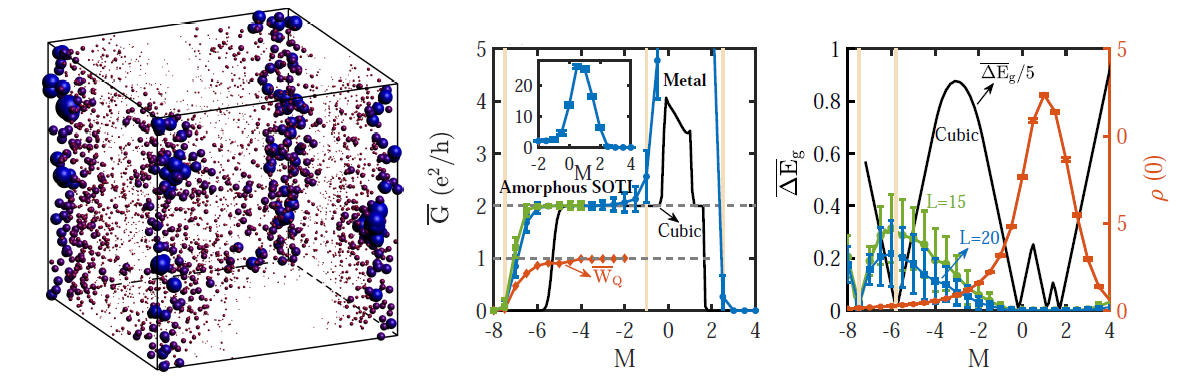
所研究體系鏈邊界態示意圖和計算結果

               在此項工作中，研究人員發現三維無定形體系中可以存在二階拓撲絕緣體，并且結構無序可以誘導出二階拓撲絕緣體。這意味著在某些條件下無定形系統相比于晶格系統更容易出現二階拓撲絕緣體。具體而言，研究人員計算了三維隨機點陣的二端電導，發現在一個參數區間內，平均電導量子化到2e² / h，表明該三維體系的棱上存在無能隙的邊界態。另外，研究人員發現這種絕緣體由四極矩的繞數保護，因此不需要晶格對稱性。研究人員還發現在一個參數范圍內，在平庸晶格體系中加入格點位置的隨機偏移會引起二端電導從0到2e² / h 的躍變。另外，隨著結構無序的增加，局域態密度表明鏈邊界態的出現。以上證據表明結構無序可以誘導出二階拓撲絕緣體。最后，研究人員考慮時間反演對稱性體系，提出兩種新的拓撲不變量在實空間刻畫二階拓撲絕緣體的性質。具體計算也表明二階拓撲絕緣體也可以存在于三維具有時間反演對稱性的無定形系統中。此項工作表明高階拓撲相可能在無定形體系中廣泛存在，對于進一步理解無序、對稱性和拓撲的關系具有重要意義。

                            

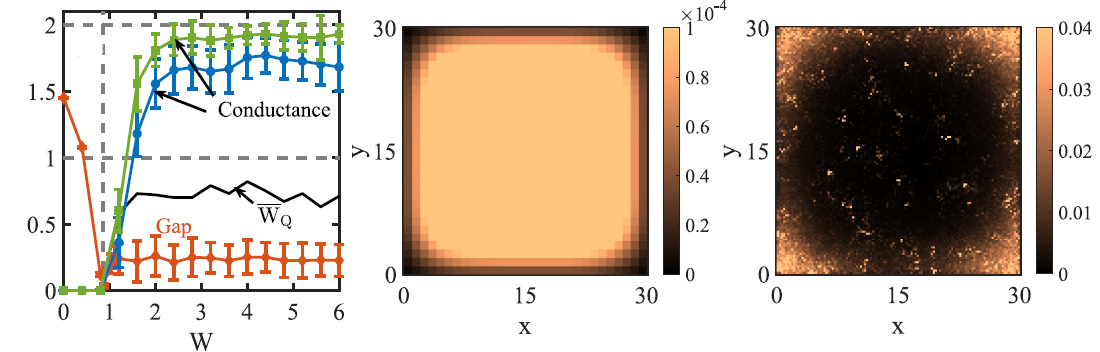
結構無序誘導的三維二階拓撲絕緣體

         該論文共同第一作者為清華大學交叉信息研究院在讀博士生王炅昊（2020級）和楊炎彬（2015級），通訊作者為徐勇助理教授，其他作者包括交叉信息研究院博士后戴凝。該項目得到國家自然科學基金、清華大學引進人才啟動經費和上海期智研究院的資助與支持。